Resolution Overview
Contents
Introduction
The spatial resolution of telescopes obtaining images from the ground is generally limited by two things -- the size of the telescope and the quality of the atmosphere ("seeing") on that night. The Palomar 5meter, for example, is a pretty darn big telescope, but the seeing is not always fabulous. The images you obtain from Palomar are often limited by the seeing, and are "smeared out" compared to what you could obtain if, say, there was no atmosphere. If there is no atmosphere, generally the most important thing in determining your spatial resolution is the size of your telescope. That, combined with the wavelength at which you are observing, gives you a diffraction limit (that is, the highest spatial resolution possible given the properties of light and the size of your telescope).
Every telescope in space can produce images limited only by the effects of diffraction -- this effect is stronger for longer wavelengths and smaller telescopes -- but diffraction will only be noticed if the camera on the telescope samples the telescope's output finely enough. Spitzer's images are diffraction-limited. Most of Spitzer's images of point sources show diffraction rings because of the telescope's small size (85 cm) and long observing wavelengths (3-160 um). In practice, what this means is that very bright sources, especially those seeen with MIPS, will appear to have rings around them - this is the first Airy ring, e.g., a result of the way the telescope responds to light of this wavelength. It's not really a ring around the object. (Wikipedia entry for Airy ring, for diffraction, and for diffraction-limited system. Consult your local intro astronomy textbook for more and/or more reliable information.)
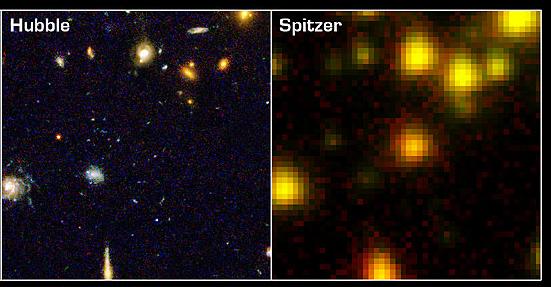
In the picture on the right (taken from this press release), you can see a (small) patch of sky imaged with Hubble (left) and Spitzer (right). The original point of this image was to show how phenomenally sensitive Spitzer is - there is a thing in the center of the Spitzer frame that is not seen by Hubble. There is something else you can learn from this image too. Look at the upper right of the Hubble image. See all the variations in size and shape of the galaxies there? Look at the same region in the Spitzer image. To Spitzer, they all look the same - similarly sized and shaped blobs. Spitzer's telescope is small (just 85 cm) and the wavelengths of light Spitzer uses are long (comparatively), so the resolution of Spitzer is limited.
Spitzer's resolution (and pixel size)
Spitzer's resolution is a strong function of wavelength. The following plot comes from the SOFIA website, and is from at least 2003 if not earlier, so Spitzer is still called SIRTF here.
The functional resolution is in practice a function of two things -- the PSF size, and the pixel size. The PSF changes as a function of wavelength, as does (in practice) the pixel size. At IRAC bands, the resolution is ~2.5". At MIPS-24, the resolution is about 6 arcsec, at MIPS-70, it's about 20 arcsec, and at MIPS-160, it's about 40 arcsec. The pixel size also increases in size from 1.2" at all four IRAC bands, to 2.55" at 24 um, to 9.96" at 70 um, to 15" (well, really 16"x18") at 160 um. These two things are not separate decisions -- with a big fat PSF at 160 um, we didn't need to have 160 um pixels as small as 1.2 arcseconds.
For those of you looking for connections between concepts... Note that, for IRAC, the PSFs are in general slightly undersampled (e.g., there are slightly less than 2 px per object). This is why PSF fitting is harder for IRAC, and why I usually use aperture photometry for IRAC. PSF fitting works great for MIPS because the PSF is very well-sampled -- there are more than a few pixels per source involved in each detection.
Comparing images of multiple wavelengths
When comparing images at different wavelengths, check that the spatial resolution is comparable! This matters, particularly for mid- and far-IR observations. You will notice this if you use images of different resolutions in a 3-color composite.
Related to this issue of resolution is the size of images that you can download using any of a number of online resources. For surveys with low spatial resolution, often the default size of the image you can download is MUCH MUCH larger than the default size of an image you can download from a survey with high spatial resolution.
Why does this matter to you? (general case)
When you are comparing the same region of space over multiple wavelengths, even within Spitzer, you need to be aware of this issue. The resolution element ("beam size") of Spitzer is so large that may in fact enclose more than one source. Because the resolution changes even within Spitzer's channels, you can find many examples of cases in which a 160 micron or 70 micron or even 24 micron source encompasses more than one IRAC source. If you look at the same region of space with something with much less spatial resolution (try IRAS or COBE/DIRBE archives), you can see that Spitzer was a huge improvement over those prior missions. If you look at the same region of space with something that has much higher spatial resolution (like HST), you will probably see some things (especially those in complicated regions) break into more pieces. This kind of comparison is of course greatly complicated when you are also comparing across wavelengths, because even the same object at the same resolution can look very different at different wavelengths. Caution is warranted!