Finding the diameter of a region we care about

Multiple ways to measure the diameter.

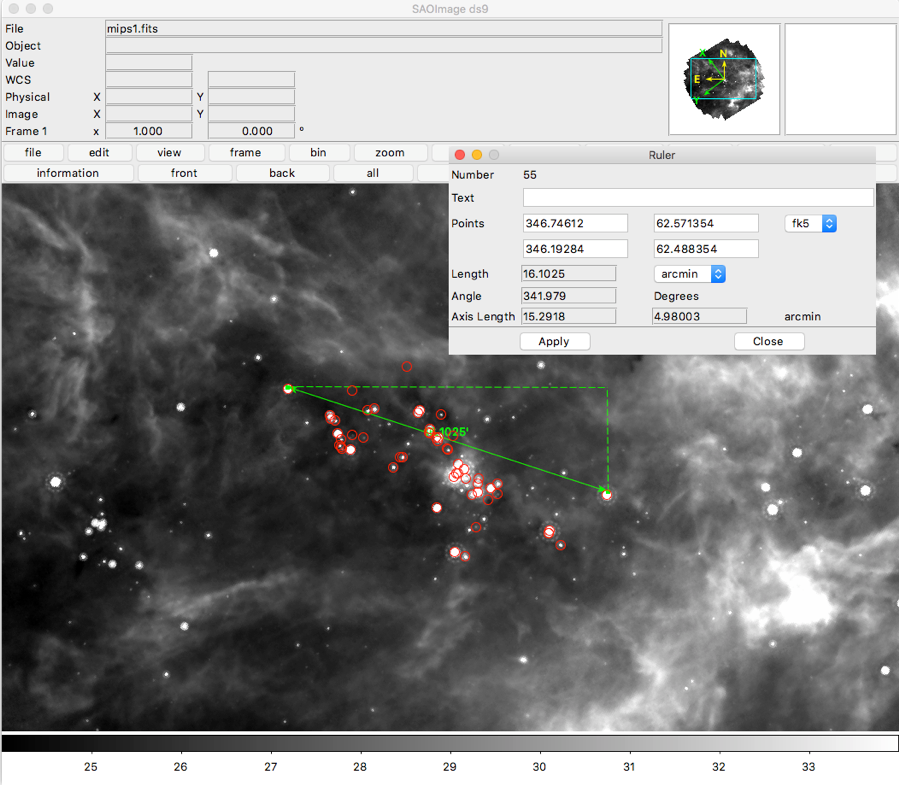
(1) load our image into ds9. Loadour regions file of interesting objects onto it. Create a region that is a ruler. Click and drag between the extremes to measure the length. Double click on the region to bring up a pop-up that shows you the length of the region you have created. Change the units if you want. I get 16 arcmin for the size of our region.

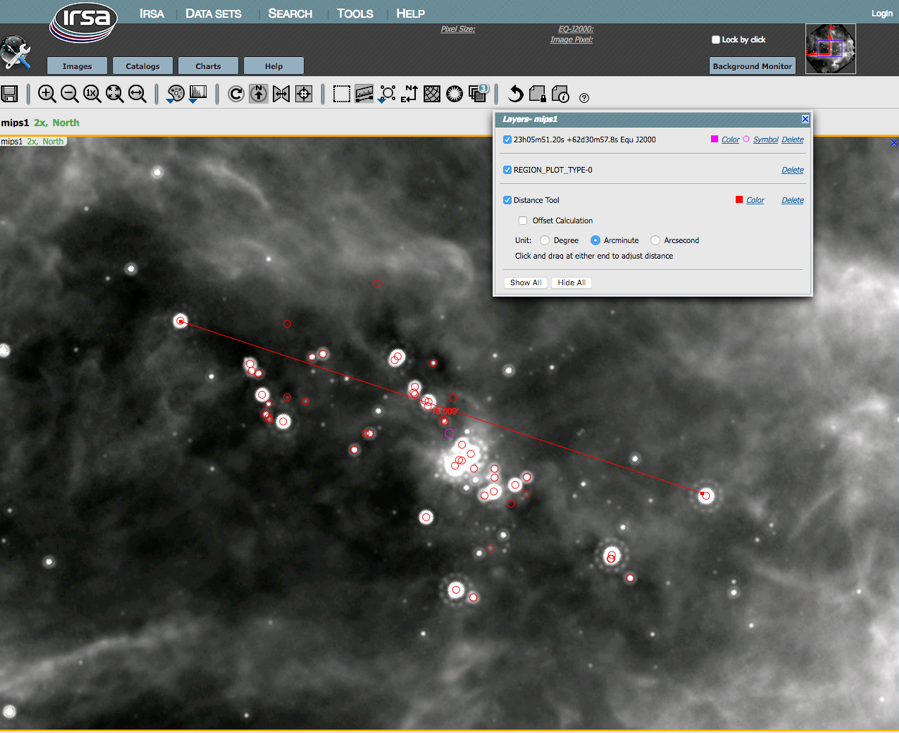
(2) Use IRSA tools to measure the length. Load an image into IRSA Viewer. Overlay the regions file of the objects of interest. Use the ruler tool to measure the length of the area. I get 16 arcmin.

(3) look at the min and max ra and dec in the file of our 54 interesting sources. Use spherical trigonometry to compute the difference. I have routines in IDL that do this for me, but you can also straightforwardly program a spreadsheet to do it. IDL> print, min(data.ra)

      346.19485

IDL> print, max(data.ra)

      346.74532

IDL> print, min(data.dec)

      62.436698

IDL> print, max(data.dec)

      62.588064

IDL> print, sphdist(min(data.ra), min(data.dec), max(data.ra), max(data.dec), /deg)

     0.29574128 (this is in degrees)

IDL> print, sphdist(min(data.ra), min(data.dec), max(data.ra), max(data.dec), /deg)*60

      17.744477 (this is in arcminutes)

So, no matter how we do it exactly, it’s always about 16-18 arcmin.

Finding the "true" size.

Now, we have a long, thin triangle:

The physical size, D, is given by the following formula: D= (θ )/206265 d where θ is the size of the object in arcseconds d is the distance to the object, an there are 206265 arcsec/radian

θ = 16 arcminutes = 16 arcmin * 60 arcseconds/arcmin = 960 arcseconds d = 700 pc D = (960 / 206265) * 700 = 3.26 pc 1 pc is 3.086x10^13 km 3.26 pc= 8.1108555e+12 km Going back to our spreadsheet from the spring, we found that the Kuiper Belt is about 6x10^9 km. So, I get ~1350 KBs across. These are not super precisely known numbers, so “about 1300 KB diameters” is just fine of an answer.